Stock Valuation based on Earnings
Stock valuation based on earnings starts out with one giant logical leap: you assume that each dollar of earnings per share of a company is really worth one actual dollar of income to you as a stockholder.
This is theoretically because you expect the company to use that dollar in a beneficial way:
for example, they could use it to pay you a dividend;
or they could invest it in their own growth, which would cause future earnings to be even greater.
You also generally assume that the company will go through several distinct phases, starting with a "growth" phase where earnings are increasing at a predictable rate, followed by a "mature" phase where earnings level off to a constant level.
To find the value of a stock, you need to calculate all of these future earnings (out to infinity!), and then use your own desired rate of return as a discount rate to find their present value.
The infinite sum of these present values is the fair market value of the stock;
or more accurately, it's the maximum price you should be willing to pay.
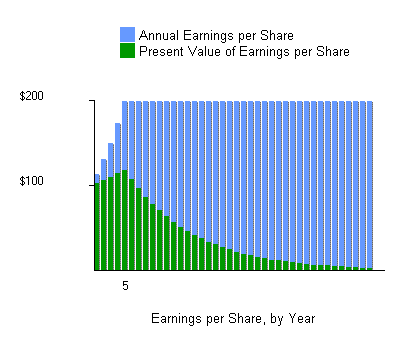
(The current fair market value is equal to the sum of the heights of all of the green bars,
which are the present values of the corresponding blue bars.)
(See more detail.)
To get the formula, we'll define some variables:
E = this year's Earnings per Share
G = growth rate of earnings (written as a decimal)
N = number of years earnings will grow
We're assuming that earnings will start to grow for N years, and then level off:
| Year | Earnings |
| 1 | E(1 + G) |
| 2 | E(1 + G)2 |
| N | E(1 + G)N |
| N + 1 | E(1 + G)N |
| N + 2 | E(1 + G)N |
Now we'll write R for our desired rate of return, and use it to find the present values of all of these earnings:
| Year | Present Value of Earnings |
| 1 | E(1 + G)/(1 + R) |
| 2 | E(1 + G)2/(1 + R)2 |
| N | E(1 + G)N/(1 + R)N |
| N + 1 | E(1 + G)N/(1 + R)N+1 |
| N + 2 | E(1 + G)N/(1 + R)N+2 |
What we've got here is two geometric series; one going from 1 to N, and the other going from N + 1 to infinity.
The result is basically too ugly to bother writing out; it's more sensible just to use the formula for the geometric series in a spreadsheet or computer program.
When people do write it out, they usually write it this way:
P = E1Q + E2Q2 + ... + ENQN + ENQN x Q/(1 - Q)
where E2 is the earnings in year 2 (or whatever) and Q is the so-called "discount factor" 1/(1 + R).
Zero-Growth Case
One special case is actually interesting to write out though.
If you assume that the stock is already in the "mature", zero-growth years -- ie, that N is zero -- the geometric series formula will simplify to:
P = E / R
or, equivalently,
P / E = 1 / R
So if you take a desired return of 11%, you find that the theoretical "fair" P/E ratio of the zero-growth stock is 1/.11 = 9.09, which sounds reasonable.
Constant-Growth Case
A second special case that people use is the "constant growth forever" case, meaning N is infinity.
The formula in this case simplifies to
P = E1 / (R - G)
where E1 is earnings over the next 12 months.
This approach can be dangerous.
Constant growth forever means the company is going to get infinitely big, which is a hard concept to fit into a common sense understanding of valuation.
The formula will give you a number as long as the growth rate G is less than the discount rate R;
but you can force it to give you a ridiculously huge number if you make G very close to R.
This graph won't let you try that - the blue bars could blow through the top of your screen and hurt somebody - but you can see it happen in the discounted cash flows calculator in the stock valuation article.
home |
article |
glossary |
calculator |
about us |
books
| 
