Compound Interest
Compound interest means getting a return on your money... and then reinvesting the return, so that your balance will keep increasing at an ever-increasing rate.
(Hence the analogy to the rolling snowball: the bigger it is, the faster it keeps getting even bigger.)
The formula for compound interest is:
Future Value = P (1 + r / n)Yn
where P is the starting principal, r is the annual interest rate, Y is the number of years invested, and n is the number of compounding periods per year.
Growth by Multiplication
Compound interest results in geometric growth (= growth by multiplication), as opposed to arithmetic growth (= growth by addition).
You can see that in the formula: after each compounding period, the balance increases by a factor of (1 + r/n).
Let's take an example with some numbers in it: $1000, invested at 5%, compounded annually.
| Balance: |
$1000.00 |
$1050.00 |
$1102.50 |
$1157.63 |
$1215.51 |
$1276.29 |
| Years: |
0 |
1 |
2 |
3 |
4 |
5 |
Each time you add 1 to years, the balance gets multiplied by 1.05.
This growth by multiplication gives the compound interest graph its familiar upward curve:
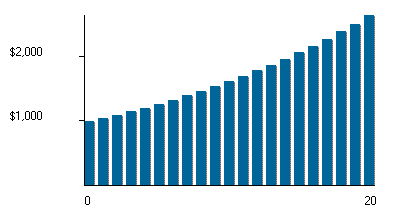
|
($1000 growing at 5%, compounded annually. The height of each bar is 1.05 times the height of the previous bar.)
|
(Simple interest doesn't do this, by the way.
It only gives you arithmetic, straight line growth.)
Compound Interest Examples
A bank account is the classic example of compound interest, since they automatically add your interest payments to your balance, compounding by default.
CAGR is a way to smooth out a complicated or volatile investment, and express the net result as if it came from compound interest at a constant growth rate.
Credit card debt is a less happy example, thanks to the high interest rates they typically charge.
You get to see that rolling snowball from the downhill side, which isn't much fun.
(So pay off those high interest debts.)
|