Also see the "real" compound interest calculator and formula.

Rule of 72 Have you always wanted to be able to do compound interest problems in your head? Perhaps not... but it's a very useful skill to have because it gives you a lightning fast benchmark to determine how good (or not so good) a potential investment is likely to be. The rule says that to find the number of years required to double your money at a given interest rate, you just divide the interest rate into 72. For example, if you want to know how long it will take to double your money at eight percent interest, divide 8 into 72 and get 9 years. Interest Rate: % Years Required for Principal to Double     Exact Answer:     Rule of 72 Estimate: (We're assuming the interest is annually compounded, by the way.) As you can see, the "rule" is remarkably accurate, as long as the interest rate is less than about twenty percent; at higher rates the error starts to become significant. You can also run it backwards: if you want to double your money in six years, just divide 6 into 72 to find that it will require an interest rate of about 12 percent. Years to double your investment Required Interest Rate     Exact Answer: %     Rule of 72 Estimate: %   Y   =   72 / r   and   r   =   72 / Y where Y and r are the years and interest rate, respectively.   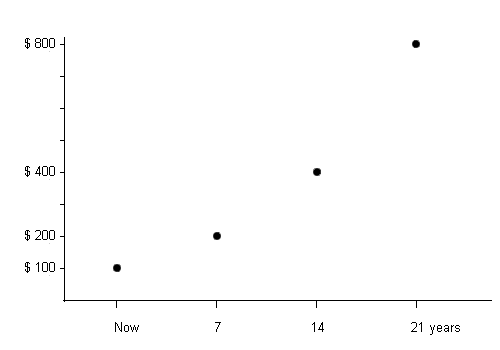Compound Interest Curve   Suppose you invest $100 at a compound interest rate of 10%. The rule of 72 tells you that your money will double every seven years, approximately:   Years Balance Now $100 7 $200 (doubles every 14 $400   seven years) 21 $800   If you graph these points, you start to see the familiar compound interest curve:     Practice using the Rule of 72 It's good to practice with the rule of 72 to get an intuitive feeling for the way compound interest works. So...     Why Stop at a Double? There's nothing sacred about doubling your money. You can also get a simple estimate for other growth factors, as this calculator shows: Find years needed for my money to ...   Double   Triple   Grow by a factor of   Estimate to Use Divide the interest rate into     Why Does the Rule of 72 Work? If you want to know more, see this explanation of why the rule of 72 works. (Brace yourself, because it's slightly geeked out.)

home  |  features  |  glossary  |  calculator  |  about us  |  books